Đạo hàm
Nội dung
Xin chào các bạn, kì thi Olympic toán sinh viên vừa qua và mình chợt nhận ra có 1 chủ đề khá hay nhưng có lẽ mọi người sẽ nghe nhiều hơn là có thể hiểu rõ nó, đó chính là ĐẠO HÀM. Bài viết hôm nay chúng ta sẽ cùng tìm hiểu nó nhé 😘😉
GÓC TOÁN HỌC KHÔNG KHÓ
Kì thi Olympic Toán học Sinh viên toàn quốc vừa mới kết thúc, lời đầu tiên AI CLUB xin được chúc mừng tất cả các thí sinh tham dự nói chung và các “mem cứng” của AI CLUB nói riêng đã hoàn thành kì thi và chắc chắn rằng ai cũng có cho mình một(hoặc nhiều) kỉ niệm đẹp về Huế mộng mơ ❤️. Xin chúc mừng các bạn đã đạt thành tích xuất sắc trong kì thi và nếu bạn còn điều gì nuối tiếc thì cũng đừng quên rằng bạn đã cố gắng hết mình rồi nè.
Nhân một dịp như thế này mình chợt nhận ra là có 1 chủ đề khá hay nhưng có lẽ mọi người sẽ nghe nhiều hơn là có thể hiểu rõ về nó, đó chính là ĐẠO HÀM.
OK Let’s go, nào chúng ta cùng tìm hiểu về nó nhaaa
Chà, đầu tiên ta cần ôn lại một vài kiến thức cơ bản chút đã nha.
Hệ số góc(tiếng anh là gradient) là gì?
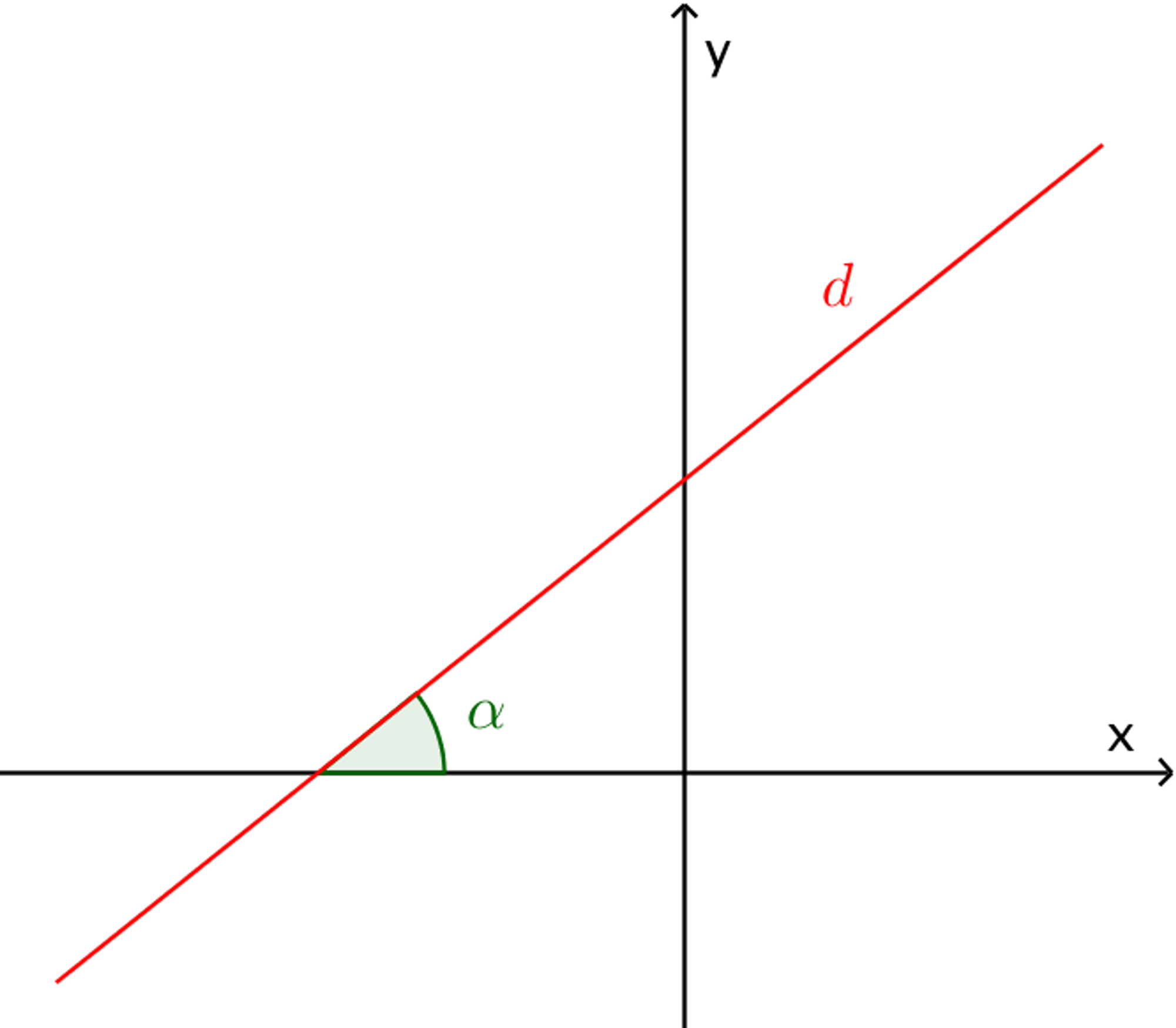
Trong mặt phẳng 0xy, hệ số góc đường thẳng (d) là a = $tan(\alpha)$, trong đó $\alpha$ là góc tạo bởi đường thẳng (d) và chiều dương của trục Ox.
Chà, đầu tiên ta cần ôn lại một vài kiến thức cơ bản chút đã nha.
Hệ số góc(tiếng anh là gradient) là gì?
Trong mặt phẳng 0xy, hệ số góc đường thẳng (d) là a = $tan(\alpha)$, trong đó α là góc tạo bởi đường thẳng (d) và chiều dương của trục Ox.
Nếu a > 0 thì $0 <\alpha < 90$
Nếu a < 0 thì $90 < \alpha < 180$
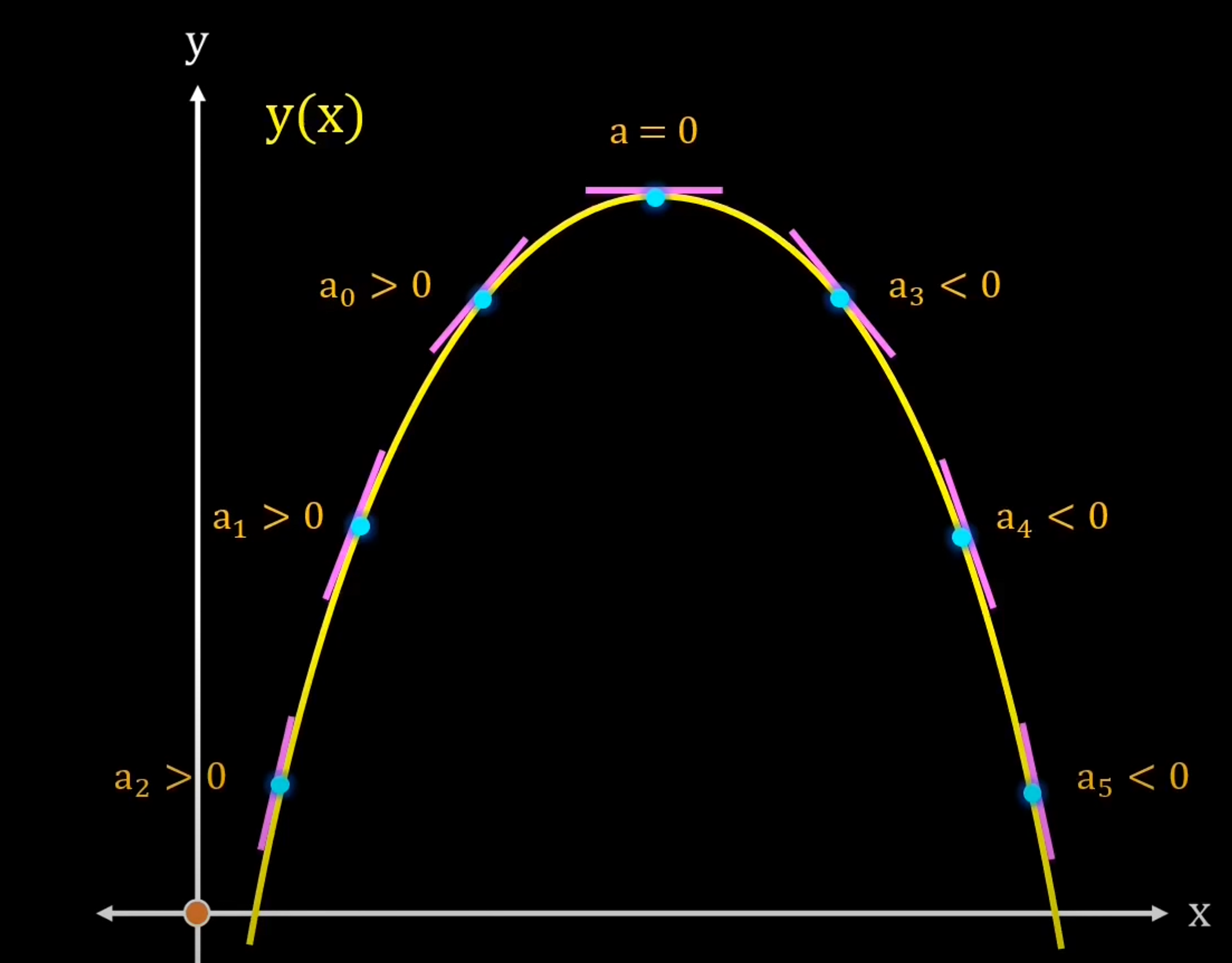
Bây giờ, ta chọn một hàm y(x) với đồ thị bất kì( để dễ nhìn thì ta sẽ chọn 1 hàm bậc 2 như hình), nhìn từ một góc nhìn khác thì đường trơn mượt y(x) đã được cấu tạo bởi nhiều đường thẳng nhỏ, mà mỗi đoạn là một tiếp tuyến với y(x).
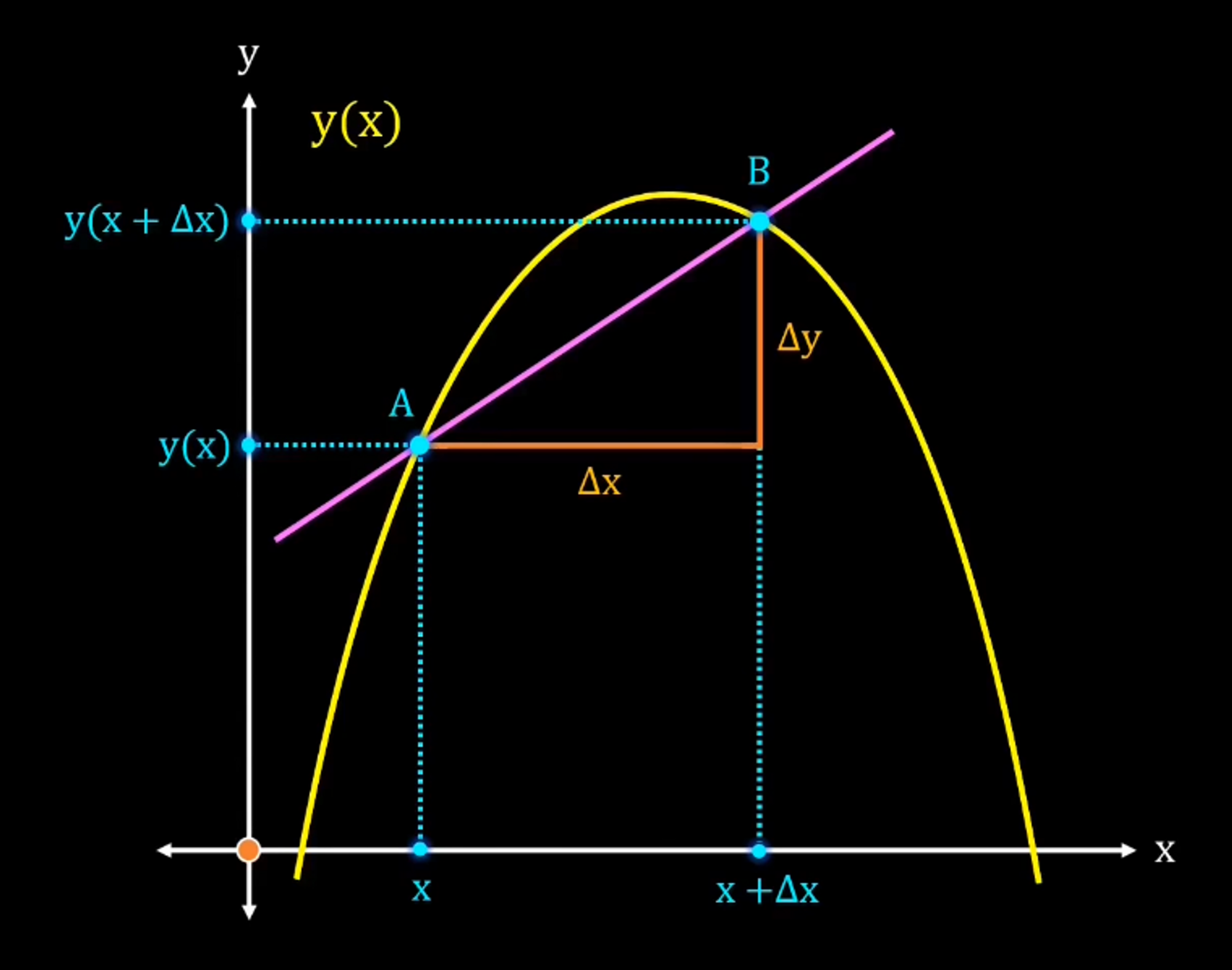
Tiếp theo ta chọn 2 điểm A(x, y(x)) và B(x+$\Delta$x, y(x + $\Delta$x)), nối 2 điểm này lại ta được đường cát tuyến AB, lập tỉ lệ ta sẽ có được độ dốc của đường cát tuyến AB là : $\begin{aligned}a = \dfrac{\Delta y}{\Delta x} = \dfrac{y(x + \Delta x) - y(x)}{\Delta x}\end{aligned}$
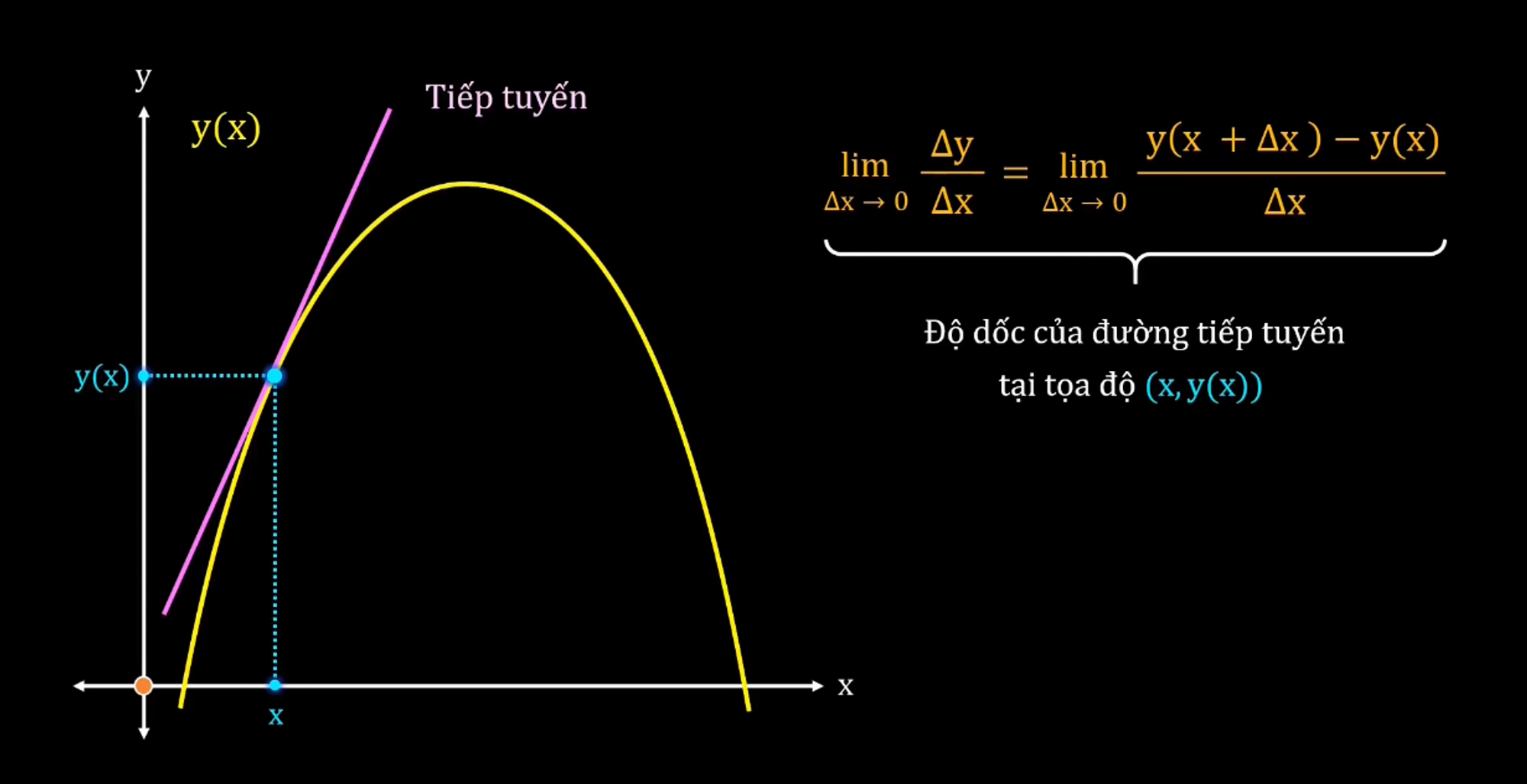
Bây giờ ta sẽ sử dụng 1 chút “magic” để biến đường cát tuyến thành tiếp tuyến nhé, ta sẽ giả sử cho $\Delta x$ → 0, có nghĩa là đoạn thẳng AB càng ngày càng ngắn đi, ngắn tới nỗi dường như 2 điểm A và B đã trùng nhau, lúc này ta đã biến đường cát tuyến AB thành đường tiếp tuyến với điều kiện cho $\Delta x $→ 0. Bây giờ công thức của chúng ta đã biến thành công thức diễn tả định nghĩa về đạo hàm mà chúng ta sử dụng ngày nay.
Chú ý rằng, $\Delta x$→ là 1 số siêu nhỏ nhưng lớn hơn 0 (vd $10^{-90}$)nhé các bạn!!!!
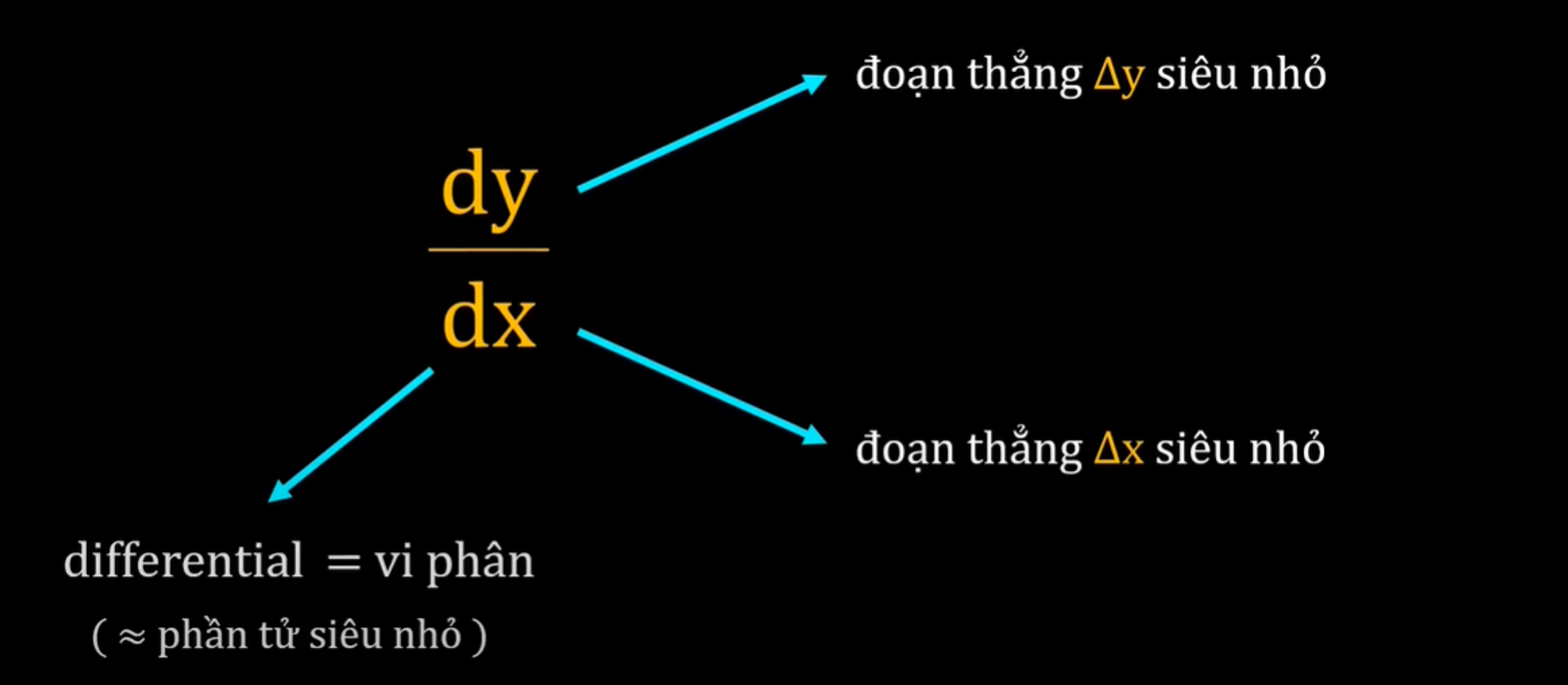
Một thông tin nữa đó là, có thể bạn chưa biết thì có 4 cách để viết kí hiệu đạo hàm luôn đó nha, và chữ d trong “dx” là d trong differential chứ không phải là derivative đâu nhé 😁

Túm cái váy lại, đạo hàm tại 1 điểm chính là đi tìm hệ số góc tiếp tuyến tại điểm đó, khi biết được hệ số góc tại điểm đó, thì ta có thể xác định được hướng của điểm đó đang đi lên hay đi xuống. Trong ML và DL, điều này rất hữu ích đấy nhé, còn hữu ích như thế nào thì AI Club hẹn các bạn vào các bài viết sau nhé hêhe
Nguồn tham khảo:
https://www.youtube.com/watch?v=HIGllE3N-iw