Markov Chain và bài toán 'Sáng nay ăn gì'
Nội dung
Trong bài viết này, chúng ta sẽ đi qua sơ lược về định nghĩa của Markov chain, từ đó hiểu thêm về Markov chain để ứng dụng vào một bài toán và thực nghiệm bằng Python.
1. Định nghĩa Markov chain
Markov chain (chuỗi Markov), được đặt theo tên nhà toán học người Nga Andrey Markov, là một mô hình ngẫu nhiên hay tiến trình ngẫu nhiên mô tả một chuỗi các sự kiện có khả năng xảy ra, mà xác suất để xảy ra sự kiện tiếp theo phụ thuộc chỉ vào sự kiện hiện tại. Đây là một mô hình “không có trí nhớ” (memorylessness), nghĩa là các sự kiện xảy ra trong quá khứ sẽ không được ghi nhớ, sự kiện trong tương lai chỉ phụ thuộc sự kiện hiện tại của mô hình.
Markov chain là sự kết hợp bởi 2 thành phần: tập trạng thái $Q$ và ma trận chuyển đổi giữa các trạng thái $P$ (ma trận này sẽ là ma trận vuông).
Ví dụ, ta định nghĩa Markov chain $\text{MC}$ có:
- Tập trạng thái là $Q = { Q_1, Q_2, Q_3 }$
- Ma trận chuyển đổi giứa các trạng thái là $\begin{aligned} P = \begin{bmatrix} P_{11} & P_{12} & P_{13} \newline P_{21} & P_{22} & P_{23} \newline P_{31} & P_{32} & P_{33} \end{bmatrix}\end{aligned}$
Markov chain $\text{MC}$ sẽ có hình dạng trông giống như một đồ thị có hướng, có trọng số, với các node trên đồ thị là các trạng thái trong tập trạng thái của Markov chain, và các trọng số trên các cạnh của đồ thị mô tả xác suất chuyển $P_{ij}$, là xác suất để di chuyển từ trạng thái $Q_i$ đến trạng thái $Q_j$. Nếu $P_{ij} = 0$, ta ngầm hiểu rằng không thể di chuyển giữa hai trạng thái $Q_i$ và $Q_j$. ⚠️ Lưu ý là các trạng thái cũng có thể quay trở về chính nó, ví dụ $P_{33}$ là xác suất để thời điểm hiện tại, Markov chain đang ở trạng thái $Q_3$ và thời điểm tiếp theo sẽ quay trở lại $Q_3$. Hình dưới đây mô tả Markov chain $\text{MC}$.
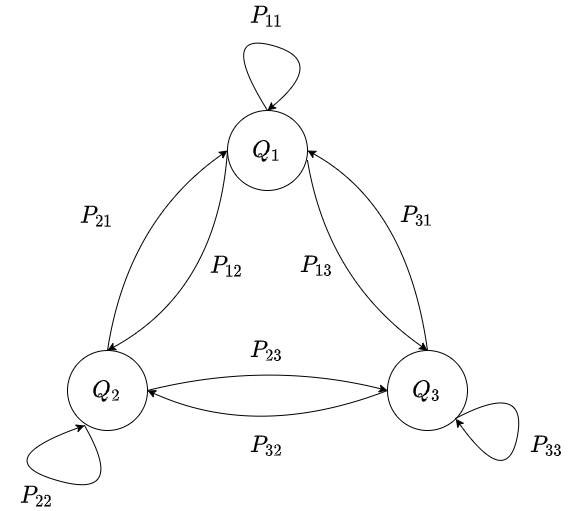
Để quan sát được đường đi của các trạng thái trong Markov chain, ta cần định nghĩa quan sát $X = (X_1, X_2, \cdots, X_t, \cdots, X_T)$ là một vector có $T$ thành phần, mô tả các quan sát của Markov chain theo thời gian, $X_t \in Q$. $X=(X_1 = Q_1, X_2 = Q_1, X_3 = Q_2, X_4 = Q_3)$ là một ví dụ về chuỗi quan sát các trạng thái của Markov chain, với xác suất xảy ra chuỗi quan sát này là tích các xác suất chuyển đổi, $P(X) = \prod_{i=1}^{T-1} X_{i}X_{i+1}$, trong ví dụ của chúng ta thì sẽ là $P(X) = P_{11}P_{12}P_{23}$, trên thực tế, ta có thể lấy logarit của $P(X)$, tạo thuận lợi cho việc tính toán, tránh bị tràn số trong các chương trình máy tính.
Cụ thể hơn về ký hiệu toán học của xác suất chuyển đổi, $P_{ij}=Pr(X_{t+1} = Q_j|X_t = Q_i)$ là xác suất để thời điểm $t$, trạng thái hiện tại của Markov chain là $Q_i$, và trạng thái của quan sát trong tương lai $t+1$ là $Q_{j}$.
2. Bài toán “Sáng nay ăn gì”
Giả sử vào một buổi sáng nọ, bạn thức dậy với 2 lần reo chuông báo thức đã qua từ điện thoại, bạn ngồi dậy, với cái bụng đang reo lên, bạn liền suy nghĩ đến việc: sáng hôm nay mình sẽ ăn gì?. Sau khi ra đầu ngõ, bạn đứng trước “ngã tư”: quán phở cô Ba, xe bánh mì cô Hai, cơm tấm chú Sáu và xe súp cua của ông Bảy. Tuy rằng, bạn đã ăn sáng mấy chục năm cuộc đời rồi, nhưng việc lựa chọn món ăn chưa bao giờ là dễ cả. May mắn thay, trong một năm vừa qua, món ăn sáng của mỗi ngày đều đã được bạn lưu trữ trên điện thoại, trong ứng dụng ghi chú (đây chính là data quý giá). Sau khi đọc định nghĩa về Markov chain ở trên, bạn quyết định áp dụng để giải quyết bài toán “sáng nay ăn gì” này.
Đó chỉ là một câu chuyện vui do tôi bịa ra để dẫn vào bài toán có thể giải quyết bằng Markov chain này. Trên thực tế, Markov chain có thể giải các bài toán to lớn hơn, nhưng trước tiên chúng ta cứ giải bài toán kia để bạn có thể lấp đầy cái bụng đã.
Trong ví dụ này, tôi sẽ hiện thực bằng Python, đọc data theo thời gian lên và tìm bộ các trạng thái $Q$, rồi tìm xác suất của ma trận $P$ kia, sau đó chọn ngẫu nhiên trạng thái (món ăn sáng) tiếp theo trên phân phối đã biết của xác suất của trạng thái (món ăn) hiện tại. Bạn có thể tải data ở đây
Đối với bộ data ở trên, tập trạng thái của chúng ta sẽ là $Q={\text{Phở}, \text{Cơm tấm}, \text{Bánh mì}, \text{Súp cua}}$
Trước tiên ta sẽ phải import các thư viện cần thiết vào Python
import numpy as np # tính toán trên ma trận
import pandas as pd # đọc dữ liệu từ file csv
from pprint import pprint # dùng cho mục đích in "đẹp"
from collections import defaultdict # để đếm số lượng lần xảy ra của các trạng thái (đơn lẻ và cặp)
Đọc dữ liệu và chuyển thành dạng list trong Python để dễ dàng sử dụng
df = pd.read_csv('breakfast.csv')
data = df.Food.tolist()
data[-5:] # xuất ra 5 món ăn cuối cùng bạn ăn
['Phở', 'Cơm tấm', 'Bánh mì', 'Phở', 'Phở']
Để có thể tạo ma trận P, trước tiên ta phải đếm các cặp và các giá trị đơn lẻ trước, sau đó đi chuẩn hóa
# tạo nơi lưu trữ giá trị
food_count = defaultdict(int)
food_pair_count = defaultdict(lambda: defaultdict(float))
Đếm các giá trị
# food_count: đếm số lần xuất hiện của một trạng thái
# food_pair_count: đếm tất cả các cặp trạng thái có thể [current][future]
n = len(data)
for i in range(n):
food_count[data[i]] += 1
if i == n - 1:
# self loop
food_pair_count[data[i]][data[i]] += 1
break
food_pair_count[data[i]][data[i + 1]] += 1
Chuẩn hóa theo tổng hàng
# chuẩn hóa theo tổng hàng
for key, value in food_pair_count.items():
for k, v in value.items():
food_pair_count[key][k] /= food_count[key] # chuẩn hóa
Do ma trận không giống như dictionary trong Python, ta chỉ có thể truy cập được bằng chỉ mục (index) của trạng thái, vì vậy ta cần phải có một dictionary lưu trữ các index của các trạng thái
# lấy index của các món ăn để dễ thao tác
keys = list(food_count.keys())
idx = range(len(keys))
key_to_idx = dict(zip(keys, idx)) # key to index
print(key_to_idx)
{'Bánh mì': 0, 'Cơm tấm': 1, 'Phở': 2, 'Súp cua': 3}
Ta bây giờ có thể tạo ma trận $P$ từ xác suất đã chuẩn hóa từ bước trên, và nên chuyển từ list sang numpy để tiện lợi cho việc tính toán hơn, do numpy là một thư viện rất mạnh của Python trong việc xử lý các thao tác liên quan đến đại số tuyến tính.
P = []
for key, value in food_pair_count.items():
P.append(list(value.values()))
# chuyển list sang numpy để dễ tính toán
P = np.array(P)
print('Ma trận chuyển trạng thái P: ')
pprint(P)
Ma trận chuyển trạng thái P:
array([[0.26582278, 0.26582278, 0.26582278, 0.20253165],
[0.25274725, 0.20879121, 0.24175824, 0.2967033 ],
[0.28571429, 0.25274725, 0.28571429, 0.17582418],
[0.25961538, 0.33653846, 0.21153846, 0.19230769]])
Ta có thể kiểm tra tổng hàng xem có bằng $1$ hay chưa, nếu chưa có thể do lỗi ở các bước trước.
# tổng hàng của ma trận phải luôn bằng 1
print(P.sum(axis=1))
[1. 1. 1. 1.] # tất cả đều 1, chuẩn
Bây giờ, phần cuối sẽ đi dự đoán món ăn. Việc dự đoán món ăn (trạng thái) tương lai khá đơn giản, ta có thể hình dung thế này: đứng ở node của trạng thái hiện tại (món ăn cuối cùng của tập dữ liệu - món ăn hôm trước), có một tập các giá trị xác suất tương ứng với trọng số của các cạnh để đi đến node khác, chọn ngẫu nhiên một node để đi đến từ tập xác suất đó (một phân phối), và ta có thể chọn ngẫu nhiên theo phân phối với hàm numpy.random.choice.
# dự đoán món ăn
curr_food = data[-1]
curr_distribution = P[key_to_idx[curr_food]]
predicted_food = np.random.choice(keys, p=curr_distribution) # random walk with known distribution
predicted_probability = P[key_to_idx[curr_food]][key_to_idx[predicted_food]]
In ra kết quả dự đoán
print(f'Món ăn chúng ta ăn hôm trước: {data[-1]}')
print(f'Món ăn nên ăn vào hôm nay là "{predicted_food}"\
với khả năng xảy ra là {round(predicted_probability * 100, 2)}%')
Món ăn chúng ta ăn hôm trước: Phở
Món ăn nên ăn vào hôm nay là "Bánh mì" với khả năng xảy ra là 28.57%
Vậy mô hình Markov chain chúng ta đã hiện thực đã dự đoán cho chúng ta món “Bánh mì” vào hôm nay.
⚠️ Lưu ý: Các giá trị, số liệu được xuất ra trong bài có thể khác, tùy thuộc vào dữ liệu cung cấp và sự lựa chọn ngẫu nhiên của các hàm trên.
Chi tiết toàn bộ code, bạn đọc có thể tham khảo ở đây
3. Tổng kết
Trên đây chỉ là một ví dụ nhỏ để mô tả khả năng của Markov chain. Ta có thể bắt gặp Markov chain trong nhiều bài toán khác như xây dựng mô hình ngôn ngữ n-gram trong lĩnh vực Xử lý ngôn ngữ tự nhiên, có thể ứng dụng vào việc Xếp hạng trang (PageRank) của Google (nhưng trên thực tế, Google sử dụng các mô hình phức tạp hơn Markov chain). Markov chain có thể phát triển lên một dạng khác, mô hình Markov ẩn, mà có thể ứng dụng trong bài toán Nhận dạng giọng nói. Và rất nhiều các ứng dụng khác trong các lĩnh vực Vật lý, Hóa học, Sinh học, Lý thuyết hàng đợi, … Bạn đọc có thể đọc thêm ở đường link này.